Find equation of the line which is equidistant from parallel lines 9x + 6y – 7 = 0 and 3x + 2y + 6 = 0.

The equations of the given lines are

9x + 6y – 7 = 0 ---------------- (1)

3x + 2y + 6 = 0 ---------------- (2)

Let P (h, k) be the arbitrary point that is equidistant from (1) and (2).

The perpendicular distance of P(h, k) from line (1) is given by

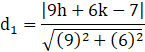
The perpendicular distance of P(h, k) from line (2) is given by

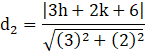
Since, P (h, k) is equidistant from lines (1) and (2),

Thus,

or

So, when is not possible as

which is not at all possible

And when

⇒ 9h + 6k – 7 = -9h – 6k – 18

⇒ 18h + 12k +11 = 0

Therefore, the required equation of the line is 18h + 12k +11 = 0.