On a common hypotenuse AB, two right triangles ACB and ADB are situated on opposite sides. Prove that ∠BAC = ∠BDC.
Given: ACB and ADB are two right triangles.
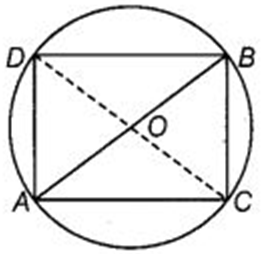
To Prove: ∠BAC = ∠BDC
Since ACB and ADB are right angled triangles, therefore
∠C + ∠D = 90° + 90°
= 180°
Therefore ADBC is a cyclic quadrilateral. (∵ Sum of opposite angles of a cyclic quadrilateral is 180°.)
Also, ∠BAC and ∠BDC lie in the same segment BC and angles in the same segment of a circle are equal.
∴ ∠BAC = ∠BDC.
Hence Proved.
8