Show that the diagonals of a parallelogram divide it into four triangles of equal area.

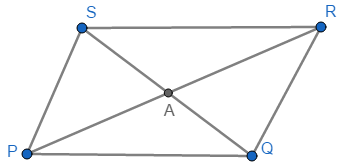
Consider parallelogram PQRS whose diagonals intersect at point A

Property of parallelogram is that its diagonal bisect each other

⇒ SA = AQ and PA = AR

Consider ΔPQS

PA is the median which divides the area(ΔPQS) into two equal parts

⇒ area(ΔPAS) = area(ΔPAQ) …(i)

Consider ΔRQS

RA is the median which divides the area(ΔRQS) into two equal parts

⇒ area(ΔRAS) = area(ΔRAQ) …(ii)

Consider ΔQPR

QA is the median which divides the area(ΔQPR) into two equal parts

⇒ area(ΔPAQ) = area(ΔRAQ) …(iii)

Using equations (i), (ii) and (iii)

area(ΔPAS) = area(ΔPAQ) = area(ΔRAQ) = area(ΔRAS)

hence, the diagonals of a parallelogram divide it into four triangles of equal area