In a ΔABC, AD is the internal bisector of ∠A, meeting BC at D.

If AB = x, AC = x–2, BD = x + 2 and DC = x–1 find the value of x.

Given: A ΔABC with AD as internal bisector of ∠A, meeting BC at D. and AB = x, AC = x–2, BD = x + 2, DC = x–1

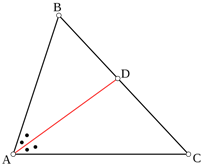
Required: The length of BC

Here, In ΔABC AD is the internal bisector of ∠A

∴ By angle bisector theorem

⇒

⇒ (x + 2)(x—2) = x(x—1)

⇒ x²—4 = x²—x (∵ (a + b)(a—b) = a²—b²)

⇒ x = 4

∴The value of x = 4cm