In a right triangle ABC, a circle with a side AB as diameter is drawn to intersect the hypotenuse AC in P. Prove that the tangent to the circle at P bisects the side BC.

Question

Philoid · Accepted Answer

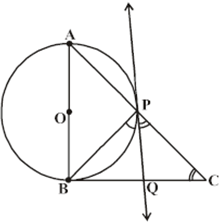
ΔABC is right angled triangle

∠ ABC = 90°

Drawn with AB as diameter that intersects AC at P, PQ is the tangent to the circle which intersects BC at Q.

Join BP.

PQ and BQ are tangents from an external point Q.

∴ PQ = BQ ---1 tangent from external point

⇒ ∠PBQ = ∠BPQ = 45° (isosceles triangle)

Given that, AB is the diameter of the circle.

∴ ∠APB = 90° (Angle subtended by diameter)

∠APB + ∠BPC = 180° (Linear pair)

∴ ∠BPC = 180° – ∠APB = 180° – 90° = 90°

Consider ΔBPC,

∠BPC + ∠PBC + ∠PCB = 180° (Angle sum property of a triangle)

∴ ∠PBC + ∠PCB = 180° – ∠BPC = 180° – 90° = 90° ---2

∠BPC = 90°

∴ ∠BPQ + ∠CPQ = 90° ...3

From equations 2 and 3, we get

∠PBC + ∠PCB = ∠BPQ + ∠CPQ

⇒ ∠PCQ = ∠CPQ (Since, ∠BPQ = ∠PBQ)

Consider ΔPQC,

∠PCQ = ∠CPQ

∴ PQ = QC ---4

From equations 1 and 4, we get

BQ = QC

Therefore, tangent at P bisects the side BC.