A square is drawn on the altitude of an equilateral triangle of side 2 metres.

i) What is the area of the square?

ii) What is the altitude of the triangle?

iii) What are the lengths of the other two sides of the triangle shown below?

(Avoid the very naming given in the following figures. As it was not there in the main problem,it is solver’s own choice)

(i) The figure is given below:

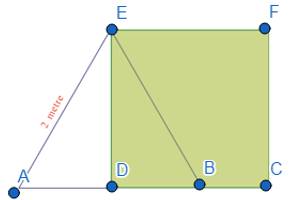
In Δ ABC,AB = BC = CA = 2 metre.

CD is the altitude. As it is a equilateral triangle, CD is also a median.

(proof: In ΔACD and ΔBCD, –

∠ADC = ∠BDC = 90⁰

AC = BC

AD is the common side

So, ΔACD≅ Δ BCD(R – H – S)

⇒ AD = BD…hence, CD is a median ,too. )

Thus, AD = BD = AB/2 = 2/2 = 1 metre

In right – angled Δ BCD,

Using Pythagoras theorem , –

….(1)

So, area of the square

(ii) altitude of the Δ ABC = CD = √3 metre [from (1)]

(iii)

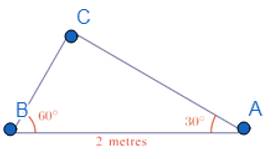
Let’s name it Δ ABC, where the angles and sides are shown in the figure.

As, we know, opposite side ofistwice than that of (can be proved by trigonometry,to be learnt in future)

⇒AC = 2BC

As ∠ACB = , using Pythagoras Theorem, –

AC² + BC² = 4BC² + BC²

= 5BC²

= BA²

= 2²

= 4

⇒ BC = √(0.8) metre

AC = 2 AC = 2 × √(0.8) metre…