The equal sides of an isosceles triangle are 8 centimetres long and the radius of its circumcircle is 5 centimetres. Calculate the length of its third side.

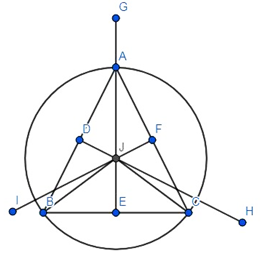
AB = AC = 8 cm

AJ = BJ = CJ = 5 cm

Let, JE = y cm and BE = x cm

In ΔJBE we have,

∠JEB = 90°

BE = x cm

JE = y cm

BJ = 5 cm

∴ x² + y² = 5²

⇒ x² = 25 – y² ……… (1)

In ΔABE we have,

∠AEB = 90°

BE = x cm

AE =(AJ + JE)=(5 + y) cm

AB = 8 cm

∴ x² + (5 – y)² = 8²

⇒ x² = 64 – (5 – y)²……… (2)

From (1) and (2) we have,

⇒ 25 – y² = 64 – (5 – y)²

⇒ 25 – y² = 64 – 25 + 10y – y²

⇒ 10y = 14

⇒ y = 1.4

Putting the value y = 1.4 in (1) we get,

⇒ x² = 25 – (1.4)²

⇒ x² = 25 – 1.96

⇒ x² = 23.04

⇒ x = 4.8

∴ Length of the third side, BC = 2x = 2 × 4.8 = 9.6 cm