In the picture below, two vertices of a parallelogram are joined to the midpoints of two sides.

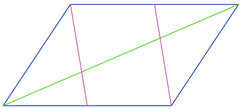
Prove that these line divide the diagonal in the picture into three equal parts.

Question

In the picture below, two vertices of a parallelogram are joined to the midpoints of two sides. Prove that these line divide the diagonal in the picture into three equal parts.

Philoid · Accepted Answer

Given ,

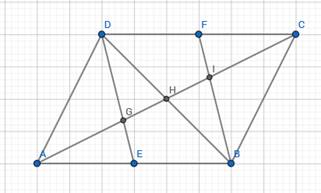
Here AC and BD are diagonals and they bisect each other as we know.

Therefore we can say that AC is the median and passes through mid-poin of DB.

We know that

In any triangle, all the medians intersect at a single point and that point divides each median in the ratio 2:1 measured from vertex.

Therefore from triangle ABD,

We have

-------1

Similarly, from triangle BCD,

We have

; ----2

From 1 & 2

AG:GI:IC = AG:(GH + HI):IC

AG:GI:IC = 2:2:2 = 1:1:1

Hence the lines from vertices to mid-points of opposite side will divide the diagonal into three equal parts as shown above.

Hence proved.

In the picture below, two vertices of a parallelogram are joined to the midpoints of two sides.Prove that these line divide the diagonal in the picture into three equal parts.

In the picture below, two vertices of a parallelogram are joined to the midpoints of two sides.

Prove that these line divide the diagonal in the picture into three equal parts.