In the picture, a circle is drawn with a line as diameter and a smaller circle with half the line as diameter. Prove that any chord of the larger circle through the point where the circles meet is bisected by the small circle.

Question

In the picture, a circle is drawn with a line as diameter and a smaller circle with half the line as diameter. Prove that any chord of the larger circle through the point where the circles meet is bisected by the small circle.

Philoid · Accepted Answer

The figure is given below. O₁ and O₂ are the centres of the big and the small circles respectively.

Now, AB is the diameter of big circle.

AO₁ is the diameter of the small circle.

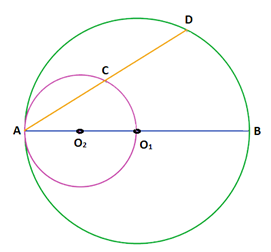
Construction:

Let us join O₁C and DB. The constructed image:

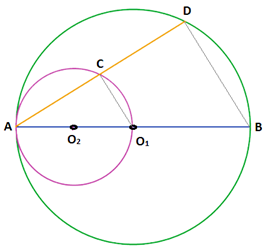
Now, since the diameter subtends a right angle in the circle at any point.

Hence, ∠ACO₁ = 90° And, ∠ADB = 90°

Now, in ΔACO₁ and ΔADB,

∠A is common to both the triangles.

AO �₁ = BO₁ (the radii of the big circle)

∠ACO₁ = ∠ADB = 90°

Hence,

in ΔACO₁∼ ΔADB,

⇒

Since, the ratio is always equal, we can say that any chord of the larger circle through the point where the circles meet is bisected by the small circle.