The numbers 1, 4, 8 on a clock’s face are joined to make a triangle.

Calculate the angles of this triangle.

How many equilateral triangles can we make by joining numbers on the clock’s face?

We know that a clock is a circle. And, a circle is made of 360°.

The clock has 12 numbers & each number represents an angle and the separation between them is

Suppose, is the clock reads, 3pm, then the angle subtended at the centre will be equal to 30° × 3 = 90°. (as shown in the figure below)

Now, the figure of the question is given below:

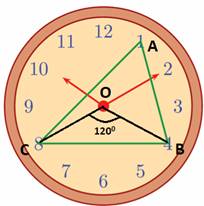
Concept involved:

Theorem (1) : The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.

Now,

∠COB = 120° (30° × 4)

From theorem (1),

The ∠CAB = 1/2 ∠COB = 60°.

And, ∠ABC = 30° × 3 = 90°.

From theorem (1), ∠ACB = 45°

Now in a triangle, all the angles sum is 180°

⇒, ∠1 + ∠4 + ∠8 = 180°

⇒ 60° +∠4 + 45° = 180°

∠4 = 75°

Hence, all the three angles are 60°, 45° and 75°.