The picture shows a triangle and its circumcircle. What is the radius of the circle?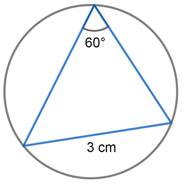

Question

Philoid · Accepted Answer

Construction, Let the centre of the circle be A and radius be r.
Let the triangle be CDE. Also, join AD and AE.

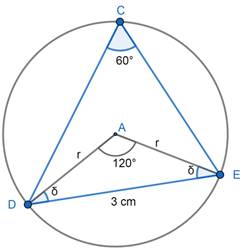
Now, AD = AE = r (radius)
We know that,
The angle formed at the centre of the circle by lines originating from two points on the circle's circumference is double the angle formed on the circumference of the circle by lines originating from the same points. i.e. a = 2b.
∴ ∠OAE = 2 (∠OCE)
⇒ ∠OAE = 2 (60°) = 120°

In Δ DAE :
Draw a perpendicular bisector on DE from A say AS.

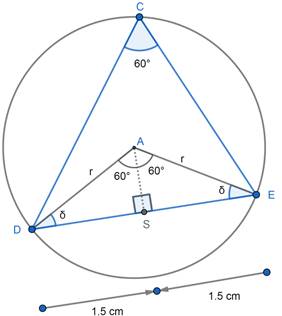
AS is a perpendicular bisector of DE.
∴ ∠DAS = ∠EAS , DS = DE and ∠ASD = ∠ASE = 90°

⇒ ∠DAE = ∠DAS + ∠EAS = 120°
⇒ ∠DAE = 2(∠DAS) = 2(∠EAS) = 120°
⇒ ∠DAS = ∠EAS = 60°

In Δ ADE,
ΔDAE is an isosceles triangle (∵ AD = AE)
∴ ∠ADE = ∠AED = δ

Now, ∠ADE + ∠DEA + ∠DAE = 180°
⇒ ∠DAE + δ + δ = 180°
⇒ 120° + δ + δ = 180°
⇒ δ = ∠ADS = 30°
We get,
∠ADS = 30° , ∠DAS = 60° and ∠DAS = 90°

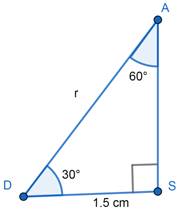
We know that sides of any triangle of angles 30°, 60° and 90°
are in the ratio 1:√3:2.

⇒ AS :DS: AD = 1: √3: 2
⇒ AS :1.5 :AD = 1: √3: 2
⇒ AD = √3 cm = r

Radius of circle is √3 cm.