The picture shows a triangle a triangle and its circumcircle. What is the radius of the circle?

Question

Philoid · Accepted Answer

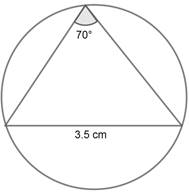
Construction, Let the centre of the circle be O and radius be r.

Let the triangle be ABC . Also, join OC and OB.

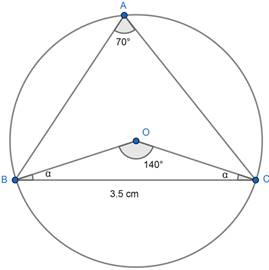
Now, OB = OC = r (radius )

We know that,

The angle formed at the centre of the circle by lines originating from two points on the circle's circumference is double the angle formed on the circumference of the circle by lines originating from the same points. i.e. a = 2b.

∴ ∠ BOC = 2 (∠ BAC)

⇒ ∠ BOC = 2 (70°) = 140°

In Δ BOC :

Draw a perpendicular bisector on BC from O say OH.

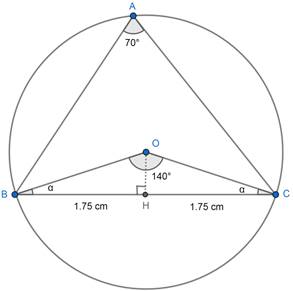
OH is a perpendicular bisector of BC.

∴ ∠ BOH = ∠ COH, OB = OC and ∠ OHB = ∠ OHC = 90°

⇒ ∠ BOC = ∠ BOH + ∠ COH = 140°

⇒ ∠ BOC = 2(∠ BOH) = 2(∠ COH) = 140°

⇒ ∠ BOH = ∠ COH = 70°

In Δ BOC,

Δ BOC is an isosceles triangle (∵ OB = OC)

∴ ∠ OBC = ∠ OCB = α

Now, ∠ OBC + ∠ OCB + ∠ BOC = 180°

⇒ α + α + 140° = 180°

⇒ 2(α) + 140° = 180°

⇒ α = ∠ OBC = 20°

We get,

∠ OBC = 20° , ∠ BOH = 70° and ∠ OHB = 90°

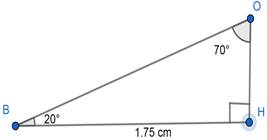
In right triangle BOH,

BH = BO × sin 70°

(From table, sin 40° = 0.939 )

BO = r = 1.86 cm

Radius of circle is 1.86 cm.