From the top and foot of a 40 m high tower, the angles of elevation of the top of a lighthouse are found to be 30° and 60° respectively. Find the height of the lighthouse. Also find the distance of the top of the lighthouse from the foot of the tower.

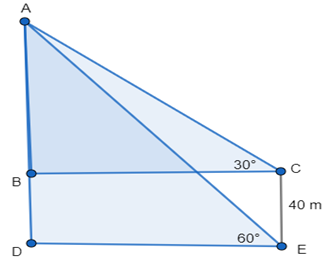
Given, CE = 40 m

Let AB = x and BD = CE = 40 m

In triangle ABC ,

∠ACB = 30°

We know,

⇒ BC = x√3 ……… (1)

And, in triangle ADE,

∠AED = 60°

We know,

……… (2)

∵ BC = DE

⇒ equation (1) = equation (2)

⇒ 3 x = x + 40

⇒ 2x = 40

⇒ x = 20

∴ Height of the tower = 40 + x

= 40 + 20

= 60 m

And, from (2)–

DE = BC

= x√3

= 20√3

And, in triangle ADE,

Also we know,

⇒ AE = 40√3 m

∴ the height of the lighthouse is 60 m and the distance of the top of the lighthouse from the foot of the tower is 40√3 m.