Derive equations of motion by graphical method.

Derivation of equations by graphical method.

Equations of motion from velocity-time graph:

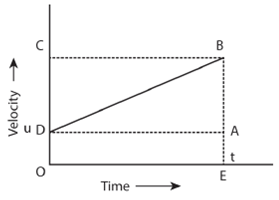
The graph shows the change in velocity with time for a uniformly accelerated object. The object starts from the point D in the graph with velocity u. Its velocity keeps increasing and after time t it reaches the point B on the graph.

The initial velocity of the object = u = OD = EA

The final velocity of the object = v = OC = EB

Time = t = OE = DA

Also from the graph we know that, AB = DC

First equation of motion

By definition, acceleration

DC = AB = at

From the graph EB = EA + AB

v = u + at

This is the first equation of motion

Second equation of motion

From the graph, the distance covered by the object during time t is given by the area of quadrangle DOEB

s = area of the quadrangle DOEB

= area of the rectangle DOEA + area of the triangle DAB

= (AE × OE) + (1/2× AB × DA)

s =

This is the second equation of motion.

The third equation of motion

From the graph, the distance covered by the object during time t is given by the area of the quadrangle DOEB.

Here DOEB is a trapezium.

Then,

S = area of trapezium DOEB

= 1/2 × sum of length of parallel side × distance between parallel sides

= 1/2 × (OD + BE) × OE

=

since

Therefore