Draw a circle of radius 2.5 centimetres. Draw a triangle of angles 40°, 60°, 80° with all its sides touching the circle.

Question

Philoid · Accepted Answer

Steps of construction:

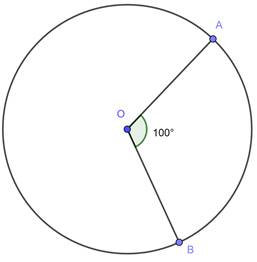
1. Draw a circle of radius = 2.5 cm with center O, take any point A on circumference and Join OB

2. Draw ∠AOB = 100°, such that point B lies on circumference.

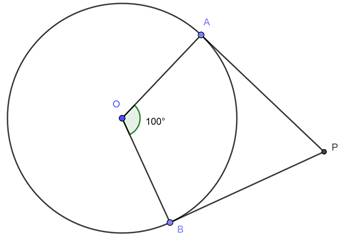
3. Draw Perpendiculars from point A and Point B such that they intersect each other at P.

4. Draw ∠AOC = 120° in the opposite direction of ∠AOB and draw perpendiculars from point A and point C such that they intersect at Q

5. Draw perpendiculars from point B and point C such that they intersect at P.

And PQR is the required triangle.

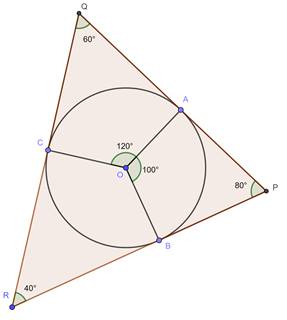
Verification of angles:

In quadrilateral AOBP

∠AOB + ∠OAP + ∠OBP + ∠APB = 360°

As,

∠AOB = 100° [By construction]

∠OAB = ∠OBP = 90° [tangent at any point on the circle is perpendicular to the radius through point of contact]

⇒ 100 + 90 + 90 + ∠APB = 360°

⇒ ∠APB = 80°

⇒ ∠P = 80°

Similarly, ∠Q = 60°

And by angle sum property of ΔPQR,

∠P + ∠Q + ∠R = 180°

⇒ 80 + 60 + ∠R = 180

⇒ ∠R = 100°