The picture shows the tangents at two points on a circle and the radii through the points of contact.

Prove that the line joining the centre and the points where the tangents meet bisects the angle between the radii.

Construction: Label the diagram.

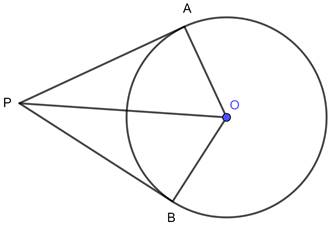
In ΔAOP and ΔBOP

OA = OB [Radii of same circle]

OP = OP [Common]

∠OAB = ∠OBP = 90° [Tangent at any point is perpendicular to the radius through point of contact]

ΔAOP ≅ ΔBOP [By Right Angle - Hypotenuse - Side Criteria]

⇒ ∠AOP = ∠BOP [Corresponding parts of congruent triangle are equal]

OP bisects ∠AOB.

i.e. the line joining the centre and the points where the tangents meet bisects the angle between the radii.