The picture shows the tangents at two points on a circle and the radii through the points of contact.

Prove that this line is the perpendicular bisector of the chords joining the points of contact.

Let us label the diagram

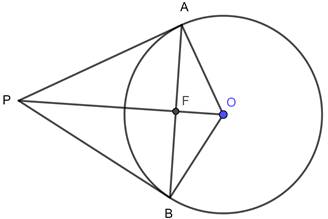
To Prove : OP is a perpendicular bisector of AB.

In ΔAOF and ΔBOF

OA = OB [Radii of same circle]

∠AOF = ∠BOF [i.e. the line joining the centre and the points where the tangents meet bisects the angle between the radii]

OF = OF [Common]

⇒ ΔAOF ≅ ΔBOF [By Side-Angle-Side Criterion]

⇒ AF = BF and ∠AFO = ∠BFO [Corresponding parts of congruent triangles are equal]

Also,

∠AFO + ∠BFO = 180° [Linear Pair]

⇒ ∠AFO + ∠AFO =180°

⇒ ∠AFO = 90°

⇒ OP ⊥ AB

And OP bisects AB

⇒ OP is perpendicular bisector of AB.