In the picture, a triangle is formed by two mutually perpendicular tangents to a circle and a third tangent.

Prove that the perimeter of the triangle is equal to the diameter of the circle.

Let us label the diagram and let the radius be 'r'.

To Prove : Perimeter of triangle PQR = diameter of circle

i.e. PQ + QR + PR = 2r

Construction: Join OA and OB

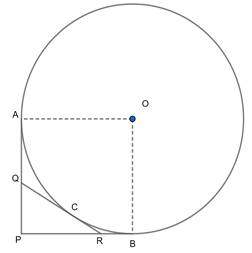
Proof:

In Quadrilateral OAPB

∠OAB + ∠APB + ∠OBP + ∠AOB = 360°

Also,

∠OAB = 90° [OA ⊥ AP, as tangent at any point on the circle is perpendicular to the radius through point of contact]

∠OBP = 90° [OB ⊥ BP, as tangent at any point on the circle is perpendicular to the radius through point of contact]

∠APB = 90° [AP ⊥ BP, Given]

⇒ 90 + 90 + 90 + ∠AOB = 360

⇒ ∠AOB = 90°

Also,

OA = OB [radii of same circle]

AP = BP [Tangents drawn from same point to a circle are equal]

And we know, if in a quadrilateral

i) All angles are 90° and

ii) Adjacent sides are equal

then the quadrilateral is square.

⇒ OAPB is a square

⇒ AP = BP = OA = OB = 'r' [radius] …[1]

Also, ⇒ as tangents drawn from same points to a circle are equal

⇒ AQ = CQ [tangents from Q] …[2]

⇒ BR = CR [tangents from R] …[3]

Also,

Perimeter of triangle PQR

= PQ + QR + PR

= PQ + QC + CR + PR

= PQ + AQ + BR + PR [From 2 and 3]

= AP + BP

= r + r [From 1]

= 2r

Hence Proved.