The picture shows a triangle formed by three tangents to a circle.

Calculate the length of each tangent from the corner of the triangle to the point of contact.

Let us label the diagram.

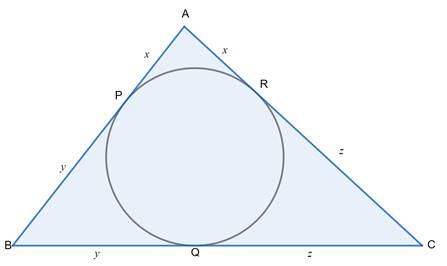
As we know that

Tangents from an external point to a circle are equal,

In given Figure we have

AP = AR = x [Tangents from point A]

BP = BQ = y [Tangents from point B]

CQ = CR = z [Tangents from point C]

Now, Given

AB = 4 cm

⇒ AP + BP = 4

⇒ x + y = 4

⇒ y = 4 - x …[1]

and BC = 7 cm

⇒ BQ+ QC = 7

⇒ y + z = 7

⇒ 4 - x + z = 7 [From 1]

⇒ z = x + 3 …[2]

and

AC = 5 cm

⇒ AR + CR = 5

⇒ x + z = 5 [From 2]

⇒ x + x + 3 = 5

⇒ 2x = 2

⇒ x = 1 cm

Putting value of x in [1] and [2]

y = 4 - 1 = 3 cm

z = 1 + 3 = 4 cm

So, we have

AP = AR = 1 cm

BP = BQ = 3 cm

CQ = CR = 4 cm