Prove the radius of the incircle of an equilateral triangle is half the radius of its circumcircle.

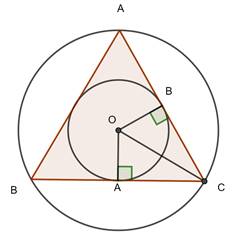
Let ABC be an equilateral triangle, its incircle and circumcircle are drawn with center O, let the radius of incircle be 'r' and circumcircle be 'R'

To prove: R = 2r

Construction: Draw OA ⊥ BC and OB ⊥ AC

Proof:

In ΔOAC and ΔOBC

∠OAC = ∠OBC [Both 90°]

OC = OC [Common]

OA = OB [Radii of incircle]

⇒ ΔOAC ≅ ΔOBC [By Right Angle - Hypotenuse - Side Criterion]

⇒ ∠OCA = ∠OCB [Corresponding parts of congruent triangles are equal]

But,

∠C = 60° [Angle of equilateral triangle]

⇒ ∠OCA + ∠OCB = 60°

⇒ ∠OCA + ∠OCA = 60°

⇒ 2∠OCA = 60°

⇒ ∠OCA = 30°

Now, In right-angled triangle OAC

[As, OA = radius of incircle = r and OC = radius of circumcircle = R]

⇒ R = 2r

Hence Proved.