Prove that in any square pyramid, the squares of the height, slant height and lateral edge are in arithmetic sequence.

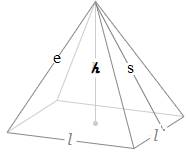
In the diagram,

e = lateral edge

s = slant height

h = height of pyramid

l = side of square base

With the help of diagram given below we get that, diagonal of square base is of length l√2

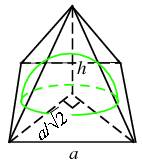
From the figures and Pythagoras theorem,

(1)

Also,

(2)

By comparing (1) and (2) we get that,

h²_, s² and e² are in AP with,

First term, a= h²

Common difference, d=

Hence, proved.