Find the number of zeros and real zeros of p(x) = x³ + 1. Show them by a graph.

Given, p(x) = x³ + 1

To find the zeros of p(x), consider p(x) = 0

∴ x³ + 1 = 0

∴ (x + 1) (x² – x + 1) = 0 Using the identity (a + b)³ = (a + b) (a² – ab + b²)

∴ x + 1 = 0 or x² – x + 1 = 0

∴ x = –1 ; real zeros of x² – x + 1 are not possible.

∴ –1 is the only zero of p(x).

Since –1 is real, number of real zeros is 1.

The given polynomial has degree 3, so it can have 3 zeros at most.

⇒ No. of zeros = 3 ; No. of real zeros = 1

For p(x) = x³ + 1, taking x = –2, –1, 0 and 2.

We obtain the following table:

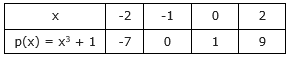
Plotting these points on graph paper, we obtain the following figure:

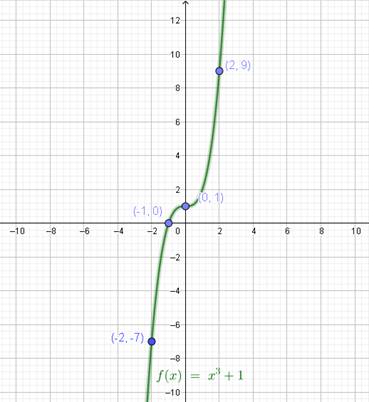
It can be seen that the graph intersects the X-axis at (–1, 0), so –1 is the zero of p(x).