The sides of a right angled triangle are consecutive positive integers. Find the area of the triangle.
Let the positive integers x, (x + 1) and (x + 2) be sides of right angled triangle
As (x + 2) will be the greatest number so (x + 2) is the hypotenuse
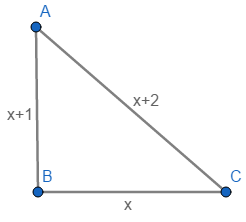
Using Pythagoras theorem
⇒ x2 + (x + 1)2 = (x + 2)2
⇒ x2 = (x + 2)2 – (x + 1)2
Using identity (a + b)(a – b) = a2 – b2
⇒ x2 = (x + 2 + x + 1)(x + 2 – x – 1)
⇒ x2 = (2x + 3)(1)
⇒ x2 = 2x + 3
⇒ x2 – 2x – 3 = 0
⇒ x2 – 3x + x – 3 = 0
taking x common from first two terms and 1 common from next two
⇒ x(x – 3) + 1(x – 3) = 0
⇒ (x + 1)(x – 3) = 0
⇒ (x + 1) = 0 or (x – 3) = 0
Thus x = 3 because x cannot be negative since x represent he side of a triangle and side cannot be a negative quantity
x + 1 = 3 + 1 = 4
x + 2 = 3 + 2 = 5
Thus, the three sides are 3, 4 and 5
As it is a right angled triangle one side would be base and the other height
Base = 3 and height = 4
Area of triangle = 
× base × height
Area of triangle = 
× 3 × 4 = 
× 12
Therefore, area of triangle is 6 unit2