Two pillars of equal height stand on either side of a road, which is 100 m wide. The angles of elevation of the top of the pillars have measure 60 and 30 at a point on the road between the pillars. Find the position of the point from the nearest end of a pillars and the height of pillars.

Question

Philoid · Accepted Answer

Let AB and DE be two pillars of equal height.

AB = DE

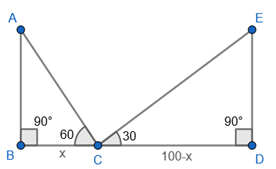
The angle of elevation of A and E from C are respectively 60⁰ and 30⁰ respectively.

∠ACB = 60⁰, ∠EDC = 30⁰ and BD = 100 m

Let BC = x

CD = BD – BC = 100 – BC = (100 – x)

In ∆ABC,

… …. (1)

In ∆EDC,

(AB = DE)

100 – x = √3AB

100√3 – AB = 3AB

4AB = 100√3

AB = 25√3

= 25 × 1.73

= 43.25 m

The height of the pillar is 43.25 m.

From equation(1),

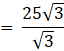
= 25

The distance of the point from the nearest end of the pillars is 25 m and the height of each pillar is 43.25 m.