A, B are the points on ⨀ (O, r) such that tangents at A and B intersect in P. Prove that OP is the bisector of ∠AOB and PO is the bisector of ∠APB.

Given that A and B are the points on (O, r) such that tangents at A and B intersect in P.

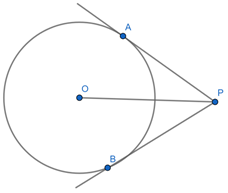
We have to prove that OP is the bisector of ∠AOB and PO is the bisector of ∠APB.

Proof:

In circle (O, r), AP is a tangent at A and BP is the tangent at B.

⇒ ∠OAP = ∠OBP = 90°

Considering ΔOAP and ΔOBP,

⇒ OA = OB (radius)

⇒ OP = OP (common segment)

∴ By RHS theorem, ΔOAP = ΔOBP i.e. OAP and OBP is a congruence.

∴ ∠APO = ∠BOP and ∠AOP = ∠BOP

Here, O is in the interior part of ∠APB and P is in the interior part of ∠AOB.

∴ OP is the bisector of ∠AOB and PO is the bisector of ∠APB.

Hence proved.