In figure 11.24, two tangents are drawn to a circle from a point A which is in the exterior of the circle. The points of contact of the tangents are P and Q as shown in the figure. A line 1 touches the circle at R and intersects and in B and C respectively. If AB = c, BC = a, CA = b, then prove that
(1) AP + AQ = a + b + c

(2) AB + BR = AC + CR = AP = AQ =

Question

Philoid · Accepted Answer

Given that AP and AQ are tangents to the circle.

A line l touches the circle at R and intersects AP and AQ in B and C respectively. And AB = c, BC = a, CA = b.

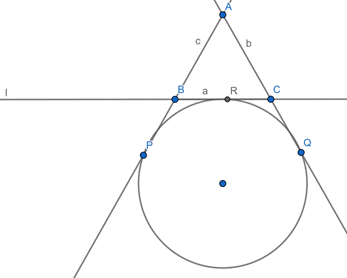
We have to prove that

(1) AP + AQ = a + b + c

(2) AB + BR = AC + CR = AP = AQ =

Proof:

By theorem,

AP = AQ, BP = BR and CQ = CR … (1)

(1) AP + AQ = (AB + BP) + (AC + CQ)

= (AB + BR) + (AC + CR) [From (1)]

= AB + AC + (BR + CR)

Since B – R – C,

⇒ AP + AQ = AB + AC + BC

= c + b + a

∴ AP + AQ = a + b + c … (2)

(2) AB + BR = AB + BP [From (1)]

= AP [∵ A – B – P]

= AQ [From (1)]

= AC + CQ [∵ A – C – Q]

= AC + CR [From (1)]

∴ AB + BR = AC + CR = AP = AQ … (3)

From (2),

⇒ AP + AQ = a + b + c

From (1),

⇒ AQ + AQ = a + b + c

⇒ 2AQ = a + b + c

⇒ AQ =

From (3),

∴ AB + BR = AC + CR = AP = AQ =

Hence proved.