A circle touches all the three sides of a right angled ΔABC in which LB is right angle. Prove that the radius of the circle is

Question

Philoid · Accepted Answer

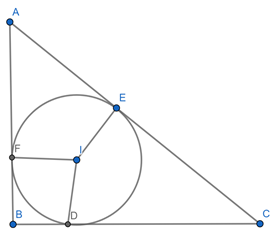
Given that a circle touches all the three sides of a right angled ΔABC.

We have to prove that radius of a circle =

Proof:

Let radius be r and the centre of the circle touching all the sides of a triangle be I i.e. incentre.

In the figure,

ID = IE = IF = r

Since ΔABC is a right angled triangle, ∠B = 90°.

Also ID ⊥ BC and AB ⊥ BC.

∴ ID || AB and ID || FB

Similarly, IF || BD

∴ IFBD is a parallelogram.

∴ FB = ID = r and BD = IF = r … (1)

∴ Parallelogram IFBD is a rhombus.

Since ∠B = 90°, parallelogram IFBD is a square.

Now AE = AF

⇒ AE = AB – FB

= AB – r [From (1)] … (2)

And CE = CD

⇒ CE = BC – BD

= BC – r [From (1)] … (3)

Now, AC = AE + CE,

⇒ AC = AB – r + BC – r

⇒ AC = AB + BC – 2r

⇒ 2r = AB + BC – AC

⇒ r =

∴ The radius of a circle is .