Two concentric circles are given. Prove that all chords of the circle with larger radius which touch the circle with smaller radius are congruent.

Question

Philoid · Accepted Answer

Given are two concentric circles.

Let two chords PQ and RS of the circle with larger radius touch the circle with smaller radius.

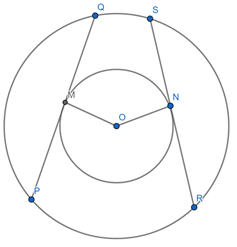
We have to prove that PQ ≅ RS.

Proof:

Let two chords PQ and RS of the circle with larger radius touch the circle with smaller radius at points M and N respectively.

PQ and RS are tangents to the circle with smaller radius,

∴ OM = ON = radius of smaller circle.

Thus, chords AB and CD are equidistant from the centre of the circle with larger radius.

∴ PQ = RS

∴ PQ ≅ RS

∴All chords of the circle with larger radius which touch the circle with smaller radius are congruent.

Hence proved.