The circumcentre of a triangle ABC is O. Prove that ∠OBC + ∠BAC = 90°.

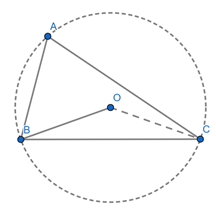
Given O is the circum centre of ΔABC.

Construction:

Join OC

We have to prove that ∠OBC + ∠BAC = 90°.

Proof:

Consider ΔOBC,

⇒ OB = OC [radii of same circle]

We know that angles opposite to equal sides are equal

⇒ ∠OBC = ∠OCB … (1)

We know that angle at the center is twice the angle at the circumference.

⇒∠BOC = 2∠BAC … (2)

We know that sum of angles of a triangle is 180°.

⇒∠OBC + ∠OCB + ∠BOC = 180°

⇒ 2∠OBC + ∠BOC = 180° [From (1)]

⇒ 2∠OBC + 2∠BAC = 180°

⇒∠OBC + ∠BAC = 180°/ 2

∴ ∠OBC + ∠BAC = 90°

Hence proved