Prove that if the bisector of an angle of a triangle and the perpendicular bisector of its opposite side intersect, then they intersect at the circumcircle of that triangle.

Question

Philoid · Accepted Answer

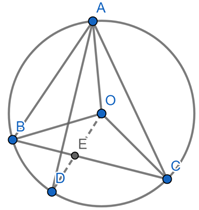
Here, O is the circumcentre of ΔABC.

Let the bisector AD of ∠A and perpendicular bisector OD of BC intersect at D.

[here perpendicular bisector passes through center because circumcenter of any triangle lies on perpendicular bisector of any of its side]

Proof:

We know that angle subtended by an arc at the centre is twice the angle subtended by the arc at the point of the alternate segment of the circle.

⇒∠BOC = 2∠A

⇒ OB = OC [Radii of same circle]

∴ ΔBOC is an isosceles triangle.

Since OD is the perpendicular bisector of BC,

We know that any three points arc always concyclic.

∴ A, C and D are concyclic.

As, AD is angle bisector,

⇒ Arc CD subtends at point A and at point O

∴ O is the centre of the circle passing through A, C and D.

Thus, the circle passing through A, C and D is the circum circle of ΔABC.

⇒ D passes through circumcircle of ΔABC

∴ They intersect the circum circle of ΔABC.

Hence proved.