In the triangle PQR, the midpoints of the sides QR and QP are X and Z respectively. The side QP is extended upto the points S so that PS = ZP. SX intersects the side PR at the point Y. Let us prove that,

Question

In the triangle PQR, the midpoints of the sides QR and QP are X and Z respectively. The side QP is extended upto the points S so that PS = ZP. SX intersects the side PR at the point Y. Let us prove that,

Philoid · Accepted Answer

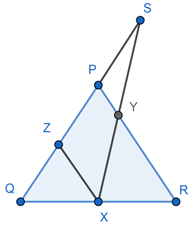
In ΔPQR, as X and Z are the midpoint of QR and PQ respectively.

So by applying the theorem:-

The line segment joining the midpoints of two side of a triangle is parallel to the third side and equal to half of it, we get,

……… (1)

Also, in ΔSZX since ZX || PY and P is the midpoint of SZ,

By applying theorem:-

Through the mid-point of any side, if a line segment is drawn parallel to second side, then it will bisect the third side and the line segment intercepted by the two sides of the triangle is equal to half of the second side.

……… (2)

From equations (1) and (2), we get