In the triangle ABC, AD is perpendicular on the bisector of ∠ABC. From the point D, a straight line DE parallel to the side BC is drawn which intersects the side AC at the point E. Let us prove that AE = EC.

Question

In the triangle ABC, AD is perpendicular on the bisector of ∠ABC. From the point D, a straight line DE parallel to the side BC is drawn which intersects the side AC at the point E. Let us prove that AE = EC.

Philoid · Accepted Answer

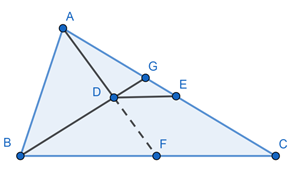
We extend the perpendicular till F such that it intersects the line BC at point F.

As BG is the angle bisector of ∠ABC,

⇒ ∠ABD = ∠FBD = θ

Since AD is perpendicular to BG, so ∠BAD = 90 – θ

In ΔABF, as sum of all sides of triangle is equal to 180°

⇒ ∠ABF + ∠BAF + ∠BFA = 180

⇒ 2θ + (90 – θ) + ∠BFA = 180

⇒ ∠BFA = 90 – θ

We know that sides opposite to equal angles in a triangle are equal and as ∠BFA = ∠BAD.

⇒ BA = BF

In ΔBAD and ΔBFD,

∠ABD = ∠FBD (given)

∠ADB = ∠FDB = 90° (given)

BA = BF (proved above)

⇒ ΔBAD ≅ ΔBFD by RHS congruency.

⇒ AD = DF, that is, D is the midpoint of AF.

Now, In ΔACF, as D is midpoint of AF and DE || FC, then by applying theorem:-

Through the mid-point of any side, if a line segment is drawn parallel to second side, then it will bisect the third side and the line segment intercepted by the two sides of the triangle is equal to half of the second side, we get,

⇒ E is the midpoint of AC

∴ AE = EC, hence proved.