In an isosceles triangle ABC, AB = AC and P is any point on produced side BC. PQ and PR are perpendicular on sides AB and AC from the point P respectively. BS is perpendicular on side AC from point B; let’s prove that PQ – PR = BS.
Given.
AB= AC;
PQ and PR are perpendicular on sides AB and AC from the point P respectively. BS is perpendicular on side AC from point B
Formula used.
Area of triangle = ![]() × Base × Height
× Base × Height
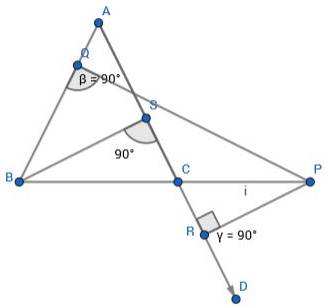
As triangle ABC and triangle ACP combines to form triangle ABP
Area of triangle ABP = Area of triangle ABC + Area of triangle ACP
Area of triangle ABP = ![]() × Base × Height
× Base × Height
![]() × AB × PQ
× AB × PQ
Area of triangle ABC = ![]() × Base × Height
× Base × Height
![]() × AC × BS
× AC × BS
Area of triangle ACP = ![]() × Base × Height
× Base × Height
![]() × AC × PR
× AC × PR
⇒ ![]() × AB × PQ =
× AB × PQ = ![]() × AC × BS +
× AC × BS + ![]() × AC × PR
× AC × PR
As AB = AC (Given)
⇒ ![]() × AC × PQ =
× AC × PQ = ![]() × AC × BS +
× AC × BS + ![]() × AC × PR
× AC × PR
Taking common ![]() ×AC get removed
×AC get removed
⇒ PQ = BS + PR
∴ PQ – PR = BS
Hence proved;