The lengths of parallel sides of a trapezium are 19 cm. and 9 cm. and the length of slant sides are 8 cm. and 6 cm. Let us calculate the area of the field in the shape of trapezium.

Given, The lengths of parallel sides of a trapezium are 19 cm. and 9 cm. and the length of slant sides are 8 cm. and 6 cm.

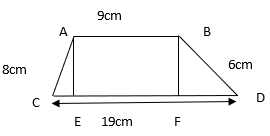
In ∆AEC,

⟹ AC²=AE²+CE² -------(i)

In ∆BFD,

⟹ BD²=BF²+FD² -------(ii)

From eq(i),

⟹ 6² = AE² +CE²⟹ AE²=36−CE²

From eq(ii),

⟹ 8²= AE² + FD² { AE = BF }

⟹ AE²=64−FD²

From figure, 19 = CE+EF+FD

⟹ CE + FD = 19−EF

⟹ CE + FD = 19−9

⟹ CE + FD = 10 ----(iii)

⟹ 36−CE²=64−FD²

⟹ 36−(10−FD)²=64−FD²

⟹ 36−100−FD²+20FD = 64−FD²

⟹ 20FD = 128

⟹ FD = 6.4cm and then CE = 10 – FD

CE = 10 – 6.4

CE = 3.6

⟹ AE² = 36−CE²

⟹ AE² = 36−3.6²

⟹ AE² = 36−12.96

⟹ AE = 4.8cm

Area of trapezium = ×(9+19)×4.8

= 67.2 sq. cm