If the length of three medians of a triangle are equal. Let us prove that the triangle is an isosceles triangle.

Question

Philoid · Accepted Answer

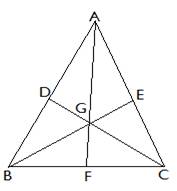
In Δ BGD and Δ CGE,

∠BGD = ∠CGE (vertically opposite angles) …(1)

BE = DC (medians are equal)

Since, centroid divides the median in ratio 2:1

So, and

⇒ BG = CG (as BE = DC) …(2)

And and

⇒ GE = DG (BE = DC) …..(3)

Hence, by SAS congruency, Δ BGD and Δ CGE are congruent.

By CPCT, BD = EC

2× BD = 2 × EC

⇒ AB = AC

Hence, the triangle is isosceles.