If the circumcentre of triangle ABC is O; let us prove that ∠OBC + ∠BAC = 90°.

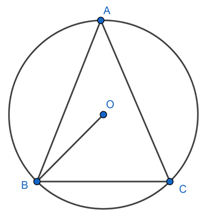
By the theorem:-

The angle formed at the centre of a circle by an arc, is double of the angle formed by the same arc at any point on circle.

As OB = OC and we know that angles opposite to equal sides are equal.

⇒ ∠OBC = ∠OCB

In ΔOBC, as sum of all sides of a triangle is equal to 180°.

⇒ ∠OBC + ∠OCB + ∠BOC = 180°

⇒ 2∠OBC + ∠BOC = 180°

⇒ 2∠OBC + 2∠BAC = 180°

⇒ ∠OBC + ∠BAC = 90°

Hence, Proved.