We drew a circle with the point A of quadrilateral ABCD as centre which passes through the points B,C and D. Let us prove that ∠CBD + ∠ CDB =

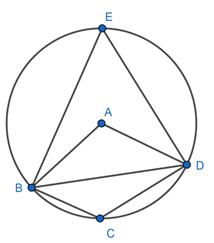
By the theorem:-

The angle formed at the centre of a circle by an arc, is double of the angle formed by the same arc at any point on circle.

∠BAD = 2 ∠BED

Since BCDE forms cyclic quadrilateral, sum of opposite angles in a cyclic quadrilateral is equal to 180°

⇒ ∠BCD + ∠BED = 180

In ΔBCD, sum of all angles is equal to 180°

⇒ ∠BCD + ∠CBD + ∠CDB = 180

Hence, proved.