In the adjoining figure, O is the centre of the circle, if ∠ACB = 30°, ∠ABC = 60°, ∠DAB = 35° and ∠DBC = x°, the value of x is

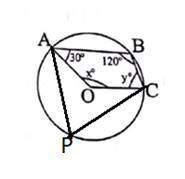
Let P be any Point in major arc of circle.

By the theorem:-

The angle formed at the centre of a circle by an arc, is double of the angle formed by the same arc at any point on circle.

⇒ x = 2 ∠APC

AS APCB is a cyclic quadrilateral, so sum of opposite sides is equal to 180°

⇒ ∠APC + ∠ABC = 180

⇒ x = 120°

Also, ABCO is a quadrilateral whose sum of interior angles is equal to 360°.

⇒ y = 360 – x – 120 – 30

⇒ y = 90°