Two circles touch each other externally at the point C. A direct common tangent AB touch the two circle at the points A and B. Value of ∠ACB is

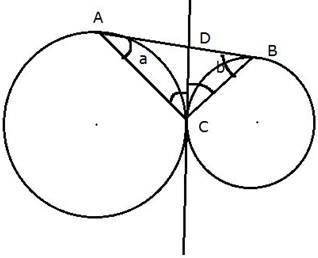
Let D be the point where the transverse tangent meets the direct tangent

∠ DAC = ∠ DCA (Tangents drawn from an external point to the same circle are always equal and hence Δ DAC is isosceles)

Let ∠ DAC = ∠ DCA = a …Equation(i)

∠ DBC = ∠ DCB (Tangents drawn from an external point to the same circle are always equal and hence Δ DBC is isosceles)

Let ∠ DBC = ∠ DBA = b …Equation(ii)

From Δ ABC we get

∠ ACB = 180⁰-(a + b)

From Equation (i) and (ii) we get

∠ DCA + ∠ DCB = (a + b)

⇒ ∠ ACB = (a + b)

Equating ∠ ACB found in the above two cases we get

180⁰-(a + b) = (a + b)

⇒ (a + b) = 90⁰

So ∠ ACB = 90⁰

So D is the correct option