The two parallel chords AB and CD with the lengths of 10 cm and 24 cm in a circle are situated on the opposite sides of the centre. If the distance between two chords AB and CD is 17 cm. then let us write by calculating, the length of the radius of the circle.

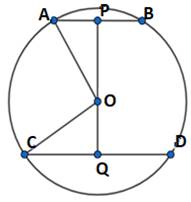
Given, AB = 10cm, CD = 24cm, PQ = 17cm

AP

Perpendicular from the center of the circle to any Chord bisects it in two line segments

AP

AP = 5cm

CQ

⇒ CQ

⇒ CQ = 12cm

In OAP, Using Pythagoras Theorem

OA² = AP² + OP²

⇒ OA² = 5² + OP²

⇒ OA² = 25 + OP² ………… (1)

⇒ In OCQ, Using Pythagoras Theorem

⇒ OC² = CQ² + OQ²

⇒ OC² = 12² + OQ²

⇒ OC² = 144 + OQ² ………. (2)

⇒ OC = OA

⇒ 144 + OQ² = 25 + OP²

⇒ OP²-OQ² = 119

⇒ (OP-OQ)(OP + OQ) = 119 (using (A² + B² = (A + B)(A-B))

⇒ OQ + OP = 17 ………. (3)

⇒ (OP-OQ)17 = 119

⇒ OP-OQ = 119/17

⇒ OP-OQ = 7 …….. (4)

Eq.3 + Eq.4

⇒ 2OP = 24

⇒ OP = 12cm

⇒ OP-OQ = 7

⇒ OQ = OP-7

⇒ OQ = 12-7

⇒ OQ = 5cm

In OAP, Using Pythagoras Theorem

⇒ OC² = 144 + OQ²

⇒ OC² = 144 + 25

⇒ OC = 13cm