If the angle-bisector of two intersecting chords of a circle passes through its centre, then let me prove that the two chords are equal.

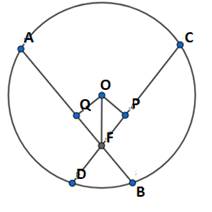
Given, OF is angle bisector of AFC.

Construction: OQ ⊥ AB and OP ⊥ CD

In ΔOFQ and ΔOFP
∠OFQ = ∠OFP (given)
OF = OF(Common)
∠OQF = ∠OPF(Construction)

AAS Congruency.
ΔOPR ≅ΔOPQ.

∴ OR = OQ (C.P.C.T)

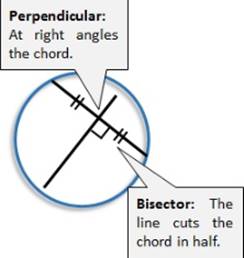
Hence AB = CD