In Fig. 9.24, ABC and ABD are two triangles on the same base AB. If line- segment CD is bisected by AB at O, show that ar (ABC) = ar (ABD).

Question

Philoid · Accepted Answer

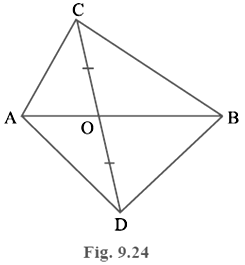
Consider ΔACD.

Line-segment CD is bisected by AB at O.Therefore, AO is the median of ΔACD

Area (ΔACO) = Area (ΔADO) (i)

Considering ΔBCD, BO is the median

Area (ΔBCO) = Area (ΔBDO) (ii)

Adding equations (i) and (ii), we get

Area (ΔACO) + Area (ΔBCO) = Area (ΔADO) + Area (ΔBDO)

Area (ΔABC) = Area (ΔABD)