XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that ar (ABE) = ar (ACF)

Question

Philoid · Accepted Answer

It is given that:

In Δ ABC, XY||BC & BE||BC & CF||AB

To prove: Ar(Δ ABE) =Ar(Δ ACF)

Proof:

Let XY intersect AB & BC at points M and N respectively.

The figure of the question is:

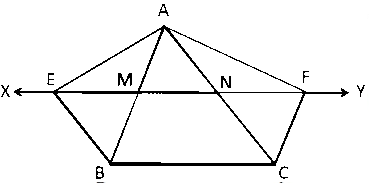
Now, XY || BC

And, we know that the parts of the parallel lines are parallel

⇒ EN || BC

Also, it is given that BE || AC

⇒ BE || CN

Therefore, BCNE is a parallelogram (because both the pair of opposite sides are parallel)

Now, the parallelogram BCNE & ΔABE have a common base i.e. BE & BE is parallel to AC.

⇒ ar(ΔABE) = ½ area of parallelogram BCNE ...(i)

Similarly, we BCFM is also a parallelogram.

And, the ΔACF and the parallelogram BCFM lie on the same base i.e. CF

⇒ ar(ΔACF) = ½ area of parallelogram BCFM ...(ii)

Now,

Parallelograms BCNE and BCFM are on the same base BC and between the same parallels BC and EF

⇒ Area (BCNE) = Area (BCFM)...(iii)

From the equations (i), (ii) and (iii), we can write that,

Ar(Δ ABE) =Ar(Δ ACF)