Construct a 3 × 3 magic square using all odd numbers from 1 to 17.

First, let us understand what magic square is.

A magic square is an arrangement of numbers in a square in such a way that the sum of each row, column, and diagonal is one constant number, the so-called “magic sum” or sometimes “magic constant”.

Collect all odd numbers from 1 to 17.

They are: 1, 3, 5, 7, 9, 11, 13, 15, 17

Now, let us try to create a magic square using these odd numbers from 1 to 17 stepwise.

Step 1: Place 1 (the smallest number is given) in the centre box in the top row.

This is where you always begin when your magic square has odd-numbered sides, regardless of how large or small that number is.

For example, in 3×3 square, you place number 1 in box 2. Similarly, if you had 11×11 square, you would have placed your number in box 6.

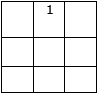
Step 2: Fill the next number, that is, number 3 to the one-upper row and to the one-right column.

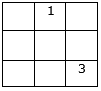
The question arises, as to why did we place number 3 in the bottom-most row?

Notice, there is no row above the row where number 1 is placed.

This is a case while placing numbers in a magic square having odd-numbered sides:

If the movement takes you to a “box” above the magic square’s top row, remain in the one right box’s column, but place the number in the bottom row of the column.

Step 3: Similarly, fill the next number 5 in the one-upper row and one-right column.

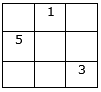
Since there is a row above the row where number 3 is placed, but no column to number 3 column’s right. We have placed the number 5 to the left-most column of the middle row.

This is another case while placing numbers in a magic square having odd-numbered sides:

If the movement takes you to a “box” to the right of the magic square’s right column, remain in the one above row, but place the number in the furthest left column of that row.

Step 4: Similarly, place the next number 7 in the one-upper row and one-right column.

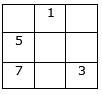
Here, we have placed 7 below 5, because there was no space for the decided movement. It was already occupied by number 1.

This is the third case while placing numbers in the magic square having odd-numbered sides:

If the movement takes you to a box that is already occupied, go back to the last box that has been filled in, and place the next number directly below it.

We have covered all the possible cases while filling odd-numbered side magic square. Now, repeat the process.

We get,

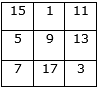
Check:

If magic sum or magic constant can be calculated using the constructed magic square, then the magic square is correct.

So, let us calculate the magic sum.

Sum of first row = 15 + 1 + 11 = 27

Sum of second row = 5 + 9 + 13 = 27

Sum of third row = 7 + 17 + 3 = 27

Sum of first column = 15 + 5 + 7 = 27

Sum of second column = 1 + 9 + 17 = 27

Sum of third column = 11 + 13 + 3 = 27

Sum of diagonal = 15 + 9 + 3 = 11 + 9 + 7 = 27

⇒ Magic sum = 27

Thus, the magic square so constructed is correct.