Show that the perpendiculars drawn from the vertices of the base of an isosceles triangle to the opposite sides are equal.

Question

Philoid · Accepted Answer

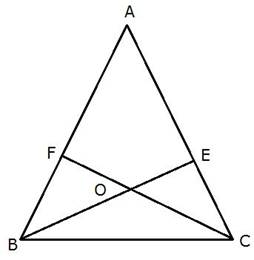
Let Δ ABC be the isosceles triangle

BE and CF are the two perpendiculars drawn which cuts at O

In Δ BFC and Δ BEC

∠FBC = ∠ECB (Base angles of isosceles triangle)

∠BFC = ∠BEC = 90⁰ (Perpendiculars)

BC = BC(Common side)

So Δ BFC and Δ BEC are congruent to each other by R.H.S. axiom of congruency

BE = FC (Corresponding Part of Congruent Triangle)

Hence its proved