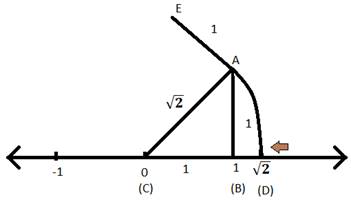
The number √2 is shown on a number line. Steps are given to show √3 on the number line using √2. Fill in the boxes properly and complete the activity.
Activity :
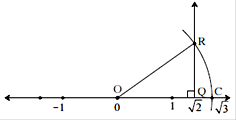
● The point Q on the number line shows the number.......
● A line perpendicular to the number line is drawn through the point Q.
Point R is at unit distance from Q on the line.

● Right angled ∆ORQ is obtained by drawing seg OR.
● l(OQ) = √2, l(QR) = 1
∴ by Pythagoras theorem,
[l(OR)]2 = [l(OQ)]2 + [l(QR)]2
= ![]() ∴ l(OR) =
∴ l(OR) = ![]()
Draw an arc with center O and radius OR. Mark the point of intersection of the line and the arc as C. The point C shows the number √3.
Activity :
● The point Q on the number line shows the number ...![]() ... .
... .
● A line perpendicular to the number line is drawn through the point Q.
Point R is at unit distance from Q on the line. (Here unit distance means 1 cm or any other unit that you choose earlier)
● Right angled ∆ORQ is obtained by drawing seg OR.
● l(OQ) = √2, l(QR) = 1
∴ by Pythagoras theorem,
[l(OR)]2 = [l(OQ)]2 + [l(QR)]2
![]()
= 3 ∴ l(OR) = ![]()
The solution for drawing ![]() :
:
To represent √3 on the number line, first of all, we have to represent √2 on the number line. The procedure for the representation of √2 will be same as shown in the activity. So, let’s start from there only. The steps further followed will be as:
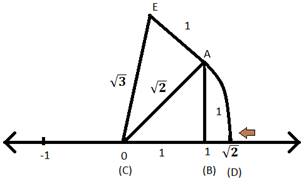
Step I: Now we need to construct a line which is perpendicular to line AB from point A such that this new line has unity length and let’s name the new line as AE.
Step II: Now join (C) and (E). The length of line CE could be found out by using Pythagoras theorem in right angled triangle EAC. So;
AE2 + AC2 = EC2
⟹ EC2 = 12 + (√2)2
⟹ EC2 = 1 + 2
⟹ EC2 = 3
⟹ EC = √3
So the length of EC line is found to be √3 units.
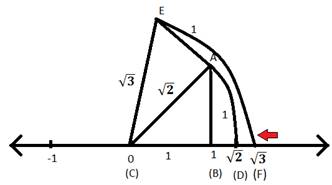
Step III: Now, with (C) as center and EC as the radius of circle cut an arc on the number line and mark the point as F. Since, OE is the radius of the arc, hence OF will also be the radius of the arc and will have the same length as that of OE. So, OF = √3 units. Hence, F will represent √3 on the number line.
Similarly, we can represent any rational number on the number line. The positive rational numbers will be represented on the right of (C) and the negative rational numbers will be on the left of (C). If m is a rational number greater than the rational number y then on the number line the point representing x will be on the right of the point represents.