Draw an obtuse-angled ∆STV. Draw its medians and show the centroid.

Question

Philoid · Accepted Answer

To draw an obtuse-angled ∆STV.

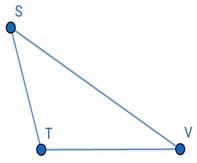
i. Draw a base line of any length, mark it TV. At T draw an obtuse angle mark that line point S. Join S and V points. ΔSTV thus formed is an obtuse angled triangle.

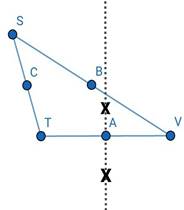
ii. Find the mid-point A of side TV, by constructing the perpendicular bisector of the line segment TV. Draw AS.

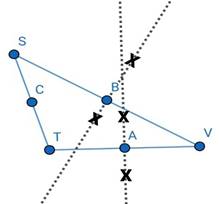
iii. Find the mid-point B of side SV, by constructing the perpendicular bisector of the line segment SV. Draw seg BT.

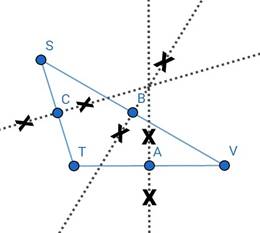
iv. Find the mid-point C of side ST, by constructing the perpendicular bisector of the line segment ST. Draw seg CV.

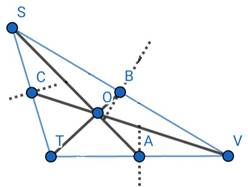
Seg AS, seg BT and seg CV are medians of ∆STV.

Their point of concurrence is denoted by O.