How to use flat cutouts to form cube, cuboids, pyramids, and cone and how to obtain a formula for volume and total surface area?
Flat Cutouts is a way of making a 3 – d figure represent in 3 – d by cutting different shapes it is made of.
(i) Cube
Each Cube consists of 6 squares with equal sides
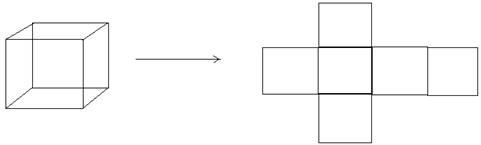
The figure above shows the flat cutouts of Cube.
Now Total Surface Area = Area of 6 squares = 6 a2
Where a = side of square.
For Volume, we will multiply the Area with the height of the surface = a2 × a = a3
(ii) Cuboid
Each Cuboid Consists of 6 rectangles having 3 dimensions namely length, breadth and height.
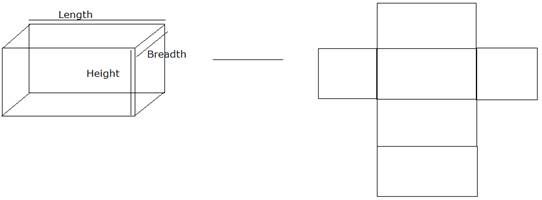
Now Total Surface Area of Cuboid = Area of all rectangles above = 2 lb + 2 bh + 2 hl
Total Surface Area = 2(lb + bh + hl)
Where, l = length, b = breadth and h = height
And Volume = Area of Rectangle × height
Volume = (l b) × h
The volume of Cuboid = lbh
(iii) Pyramid
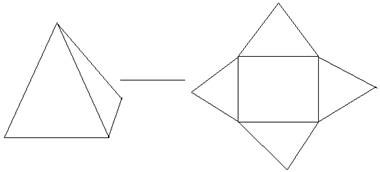
Total Surface Area = Area of Four Triangles + Area of Square
Total Surface Area = 1/2 h a + 4 a
(where h = height of Pyramid and a = side of base)
Volume of Pyramid = Area of Base × 1/3 height
Volume of Pyramid = 1/3 a2 h
(iv) Cone
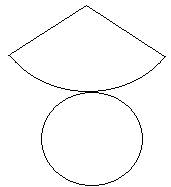
The figure above shows the cutout of Cone
Total Surface Area of Cone = Lateral Surface Area of Cone + Area of Base
Total Surface Area of Cone = π r l + π r2
Where l = slant height of cone and r is the radius of the base
Total Volume of Cone = 1/3 π r2 h
Where h = height of the cone.