Two parallel sides of an isosceles trapezium are 6 cm and 14 cm respectively. If the length of each non-parallel side is 5 cm find the area of the trapezium.
The figure is given below:
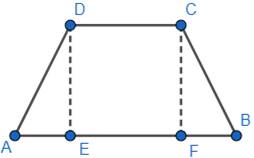
According to the question,
AB = 14 cm DC = 6cm. Also AD = BC = 5 cm
(∵ trapezium is isosceles)
Also, DC = EF can be seen from the figure.
Also AE = FB = x
So we can say
AE + EF + FB = AB
x + 6 + x = 14
2x = 8
∴ x = 4.
⇒ AE = FB = 4.
Now in ΔAED,
∠ AED = 90°
∴ By pythogares theorem
We get
(AD)2 = (AE)2 + (ED)2
(5)2 = (4)2 + (ED)2
(ED)2 = 25–16 = 9
∴ ED = 3
Hence distance between two parallel sides is 3 cm.
Area of the trapezium is given by
= 
×(sum of parallel sides)×(distance between them)
= 
= 
= 30cm2
∴ The area of a trapezium is 30cm2.
6