Prove that tan20° tan40° tan60° tan80° = 3
FORMULA: -
(i) ![]()
(ii) tan60° = √3,
![]()
cos90° = 0, and
![]()
(iii) 2sinAsinB = cos(A – B) – cos(A + B)
(iv) 2cosAsinB = Sin(A + B) – Sin(A – B)
tan20° tan40° tan60° tan80° ![]()
⇒ tan20° tan40° tan60° tan80° ![]() - - -
- - -
⇒ tan20° tan40° tan60° tan80° ![]()
⇒ tan20° tan40° tan60° tan80° ![]()
using formula(ii)
⇒ tan20° tan40° tan60° tan80° 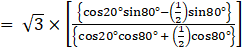
multiplying with 2
⇒ tan20° tan40° tan60° tan80° 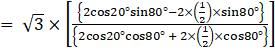
using formula(iv)
⇒ tan20° tan40° tan60° tan80° ![]()
⇒ tan20° tan40° tan60° tan80°![]() -
-
using formula(iii)
⇒ tan20° tan40° tan60° tan80° 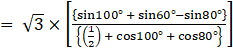
tan 20° tan 40° tan 60° tan 80° 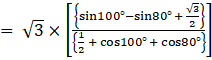
⇒ tan20° tan40° tan60° tan80° 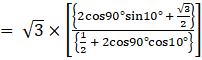
⇒ tan20° tan40° tan60° tan80° 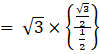
⇒ tan20° tan40° tan60° tan80° ![]()
⇒ tan20° tan40° tan60° tan80° = 3
12